Bohlen-Pierce Scale
This page has a lot of information about the Bohlen-Pierce Scale, and I hope you enjoy going through it. Listen to some Bohlen-Pierce Scale music as you read!
The Bohlen-Pierce Scale has become one of the most well-known xenharmonic (nonstandard) musical tunings worldwide, even though it's one of the most difficult to write music with. It is a tuning of intrigue, both in its incredible history and also its mathematical structure. It's one of the oddest tunings, yet it is mathematically cleaner than the standard 12-tone tuning of most instruments across the globe.
Instead of 12 notes per octave, the Bohlen-Pierce Scale is 13 notes per tritave (more details on what a tritave is later). It's a macrotonal tuning, meaning the steps are larger than half steps that musicians are used to. It's also a nonoctave tuning, meaning.. no octaves!
Of all the crazy things, two microwave engineers–Heinz Bohlen and John R. Pierce independently invented the scale several years apart. Somewhere in between, so did a computer artist and theorist named Kees Van Prooijen. Below, you can read about the history of the Bohlen-Pierce Scale, find my research, learn about some modes and chords, and, most importantly, listen to more Bohlen-Pierce Scale music!
From the beginning
Not all music is composed with the same notes and chords that pianos and guitars can play, based on octaves divided into 12 steps each. Xenharmonic music uses tunings containing more or less notes than the usual 12 notes per octave.
The Bohlen-Pierce Scale (BP) takes it a step further and doesn't even use an octave as the frame. Having no octaves in BP means we have only one of every note across the hearing range. That's a pretty crazy concept for a musician to work with. For example, we're used to doubling up a bass line an octave down from the guitar chords or adding lushness to sounds by doubling the chords an octave higher. You can throw these standard compositional techniques out the window when composing in BP!
What is an octave, you ask?
An octave is the musical interval of two notes, where the waveform of the higher note is 2x the frequency of the lower note. They sound like the same note, except one is higher. Think of a child and their dad singing the same melody together. They'd be naturally singing an octave or two apart. For example, all C's across a musical instrument are octaves apart, all A's are octaves apart, etc. (You'll see later that this correspondence between note letter names and octaves doesn't exist in BP.)
Since the frequency doubles with each octave, the frequency grows exponentially as we play octaves sequentially from low to high. But to humans, each doubling sounds like the same interval size. [Fun fact: We hear logarithmically, which linearizes the exponentiality of the frequency doubling. I wonder what else works this way in the physical versus physiological world.] The fact that octaves are all the same physical distance apart on a piano reflects how we hear them.
So not only do notes sound higher as they climb up, but they spiral around with each octave, like flights of stairs that have a landing on each floor. Another comparison is our numbering system. Think about how 10 is the frame for our standard decimal numbering system versus how an octave is the frame for most musical scales. Consider what it feels like as we count up in our numbering system. We launch off, "1, 2, 3…" and something special happens as we anticipate landing on 10, then launch off again. We always anticipate getting to the next multiple of 10, such as "17, 18, 19... 20!" Then we can launch off of 20. It's also a different feeling counting down.
The feeling of music is the same idea and even more pronounced. We anticipate the next octave as we play up the notes of a scale. Landing on an octave can feel like a resting position from which we can launch back off. Musical tunings are also generally framed by octaves divided into some manageable number of notes, like how the frame of our decimal system (10) is divided equally into ten equal divisions (0-9).
If not an octave, then what frame does the Bohlen-Pierce Scale use? The Bohlen-Pierce Scale uses a frame called a tritave!
Sorry, octaves, we're using a tritave instead!
Just take a moment to feel the humor of this. Who in their right mind would overlook the octave when making a new tuning for musicians? Two microwave engineers! That's who! I'm sorry, but I think that's so funny. Heinz Bohlen himself told me that it didn't occur to him that musicians would miss the octave so much. Actually, we don't because it's a fun challenge, and the scale is worth it! Kees Van Prooijen, to his defense, was exploring multiple nonoctave tunings on purpose. And as for Heinz Bohlen and John R. Pierce, mathematics led them to use the tritave. It's also the perfect opportunity for all kinds of psychoacoustical research.
What IS a tritave?
Trained musicians will hear a tritave as "an octave and a fifth." Whereas an octave is an interval of 2x the frequency, a tritave is 3x the frequency. In the case of the Bohlen-Pierce Scale, as we play up the steps in the scale, we should anticipate the next tritave–or so we'd hope. But, unlike the octave, the two notes of a tritave don't have the same pitch class. In other words, they don't sound like the same note, like octaves do, and don't have that same "pull" on our brains. Since humans are generally wired to perceive octaves as the frame when we hear music, we find it harder to experience the same anticipation and satisfaction with tritaves.
This tritave frame is divided into 13 steps to make the Bohlen Pierce Scale. So we say the Bohlen-Pierce Scale is '13 notes per tritave' instead of the usual 12 notes per octave. One consequence is that each step is slightly larger than we're used to. [A semi-tone in BP sounds somewhere between a semi-tone and whole-tone in a 12-tone tuning, whereas a whole tone in BP sounds like a minor third in 12-tone. The fact that a whole-tone sounds like a standard minor third is why we hear minor 7th chords all over the place in BP music. Don't worry if you don't know what any of that means!]
Remember how I said above that tritaves were hard to hear as the frame of the tuning? I'm convinced now that it may not be the case for anyone born and raised listening to the Bohlen-Pierce Scale or even anyone who intensely composes tonal Bohlen-Pierce Scale music over a long period. I say tonal because avant-garde or otherwise atonal music will not train your ear to hear the tritave as the frame. The tonality of organized chords and melodies will eventually coax our neurons to form the new connections we need to perceive the tritave as taking on the function of an octave.
Our neurons do what?
Our brains naturally have dynamical attractors (cooperating neurons) that pull on us when music lands on octaves, and other harmonic intervals to a lesser degree, to give us a feeling of stability and resolution. Whether musically trained or not, humans are wired to hear the octave as the main frame of reference. But if we deprive ourselves of octaves and instead immerse ourselves in an alien tuning that is not only devoid of octaves but also musically uses a different frame, our brains will eventually compensate.
One day, after immersing myself in tonal Bohlen-Pierce Scale music for many years, I heard the tritave as an octave, which scared me! It didn't just take on the function of an octave–it sounded like an octave. I thought I must be overly tired. But this has happened several times since then. Nowadays, almost every time I compose a new song in BP, I experience this phenomenon. I'll ask myself, "How did an octave sneak into the music?" thinking my synths need to be re-tuned. And then I realize, "Oh wow, that's a tritave! BP has broken my brain!" I go through this ridiculous thought process every time. It's as if my subconscious brain has grown new connections, but my aware brain is still uncomfortable with it. So, each time now, I'll take a moment to hear the tritave as its own interval while embracing its function as the frame.
Don't worry. You won't lose your ability to hear an octave as the frame in other tunings! That's a hard wiring.
One conclusion I've made is that it must be more critical that there IS a frame and less important as to what it is. Listen to tonal Bohlen-Pierce Scale music long enough, and you may someday hear the tritave act like an octave. It's an extraordinary feeling.
Here is the main Bohlen-Pierce Scale website, formerly run by Heinz Bohlen.
Bohlen-Pierce Modes and Tunings

Some modes and chords are mapped out here, which you may find useful.
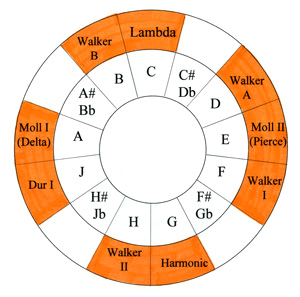
I will always cherish this image from the website. It's the Lambda family wheel that Heinz Bohlen drew in 2001. Read the fun story about it here.
Elaine Walker
Involution | Involution YouTube (2023, Elaine Walker / No Terrestrial Road)
Magic Rectangle (2021, Elaine Walker / Four-Momentum)
Infinity | Infinity video performance (2019, Elaine Walker / Four-Momentum)
Euler's Identity (2018, Elaine Walker / Four-Momentum)
Love Song | Love Song live performance at Berklee | Love Song YouTube (2011, ZIA / Drum'n'Space)
Greater Good | Greater Good practicing at home | Greater Good YouTube (2011, ZIA / Drum'n'Space)
1-rx^2 Part1 | Part2 | Part3 | Part4 (1992, composed in MAX using Chaos Melody Theory)
Agribusiness (1992, ZIA / v1.5)
Stick Men | Stick Men live performance at Berklee (1992, ZIA / v1.5)
Dr. Richard Boulanger
I Know of No Geometry
Solemn Song for Evening (live performance at the Bohlen-Pierce Symposium 2010)
Sevish
Orbital (Bohlen-Pierce beat)
Mashroon (microtonal drum & bass, Bohlen Pierce scale)
Find more music on the main Bohlen-Pierce Scale website.
My lecture at the Bohlen-Pierce Scale Symposium, Boston 2010: 5 Videos
AXIS keyboard for the Bohlen-Pierce Scale: 11 Videos
Building a Bohlen-Pierce Scale Vertical Keyboard: 1 Video
Hearing Inversions in BP – Listening Examples: 4 Videos





Bohlen-Pierce keyboards are discussed here, as well as featured in the above videos.
The Bohlen-Pierce Scale has become one of the most well-known xenharmonic (nonstandard) musical tunings worldwide, even though it's one of the most difficult to write music with. It is a tuning of intrigue, both in its incredible history and also its mathematical structure. It's one of the oddest tunings, yet it is mathematically cleaner than the standard 12-tone tuning of most instruments across the globe.
Instead of 12 notes per octave, the Bohlen-Pierce Scale is 13 notes per tritave (more details on what a tritave is later). It's a macrotonal tuning, meaning the steps are larger than half steps that musicians are used to. It's also a nonoctave tuning, meaning.. no octaves!
Of all the crazy things, two microwave engineers–Heinz Bohlen and John R. Pierce independently invented the scale several years apart. Somewhere in between, so did a computer artist and theorist named Kees Van Prooijen. Below, you can read about the history of the Bohlen-Pierce Scale, find my research, learn about some modes and chords, and, most importantly, listen to more Bohlen-Pierce Scale music!
From the beginning
Not all music is composed with the same notes and chords that pianos and guitars can play, based on octaves divided into 12 steps each. Xenharmonic music uses tunings containing more or less notes than the usual 12 notes per octave.
The Bohlen-Pierce Scale (BP) takes it a step further and doesn't even use an octave as the frame. Having no octaves in BP means we have only one of every note across the hearing range. That's a pretty crazy concept for a musician to work with. For example, we're used to doubling up a bass line an octave down from the guitar chords or adding lushness to sounds by doubling the chords an octave higher. You can throw these standard compositional techniques out the window when composing in BP!
What is an octave, you ask?
An octave is the musical interval of two notes, where the waveform of the higher note is 2x the frequency of the lower note. They sound like the same note, except one is higher. Think of a child and their dad singing the same melody together. They'd be naturally singing an octave or two apart. For example, all C's across a musical instrument are octaves apart, all A's are octaves apart, etc. (You'll see later that this correspondence between note letter names and octaves doesn't exist in BP.)
Since the frequency doubles with each octave, the frequency grows exponentially as we play octaves sequentially from low to high. But to humans, each doubling sounds like the same interval size. [Fun fact: We hear logarithmically, which linearizes the exponentiality of the frequency doubling. I wonder what else works this way in the physical versus physiological world.] The fact that octaves are all the same physical distance apart on a piano reflects how we hear them.
So not only do notes sound higher as they climb up, but they spiral around with each octave, like flights of stairs that have a landing on each floor. Another comparison is our numbering system. Think about how 10 is the frame for our standard decimal numbering system versus how an octave is the frame for most musical scales. Consider what it feels like as we count up in our numbering system. We launch off, "1, 2, 3…" and something special happens as we anticipate landing on 10, then launch off again. We always anticipate getting to the next multiple of 10, such as "17, 18, 19... 20!" Then we can launch off of 20. It's also a different feeling counting down.
The feeling of music is the same idea and even more pronounced. We anticipate the next octave as we play up the notes of a scale. Landing on an octave can feel like a resting position from which we can launch back off. Musical tunings are also generally framed by octaves divided into some manageable number of notes, like how the frame of our decimal system (10) is divided equally into ten equal divisions (0-9).
If not an octave, then what frame does the Bohlen-Pierce Scale use? The Bohlen-Pierce Scale uses a frame called a tritave!
Sorry, octaves, we're using a tritave instead!
Just take a moment to feel the humor of this. Who in their right mind would overlook the octave when making a new tuning for musicians? Two microwave engineers! That's who! I'm sorry, but I think that's so funny. Heinz Bohlen himself told me that it didn't occur to him that musicians would miss the octave so much. Actually, we don't because it's a fun challenge, and the scale is worth it! Kees Van Prooijen, to his defense, was exploring multiple nonoctave tunings on purpose. And as for Heinz Bohlen and John R. Pierce, mathematics led them to use the tritave. It's also the perfect opportunity for all kinds of psychoacoustical research.
What IS a tritave?
Trained musicians will hear a tritave as "an octave and a fifth." Whereas an octave is an interval of 2x the frequency, a tritave is 3x the frequency. In the case of the Bohlen-Pierce Scale, as we play up the steps in the scale, we should anticipate the next tritave–or so we'd hope. But, unlike the octave, the two notes of a tritave don't have the same pitch class. In other words, they don't sound like the same note, like octaves do, and don't have that same "pull" on our brains. Since humans are generally wired to perceive octaves as the frame when we hear music, we find it harder to experience the same anticipation and satisfaction with tritaves.
This tritave frame is divided into 13 steps to make the Bohlen Pierce Scale. So we say the Bohlen-Pierce Scale is '13 notes per tritave' instead of the usual 12 notes per octave. One consequence is that each step is slightly larger than we're used to. [A semi-tone in BP sounds somewhere between a semi-tone and whole-tone in a 12-tone tuning, whereas a whole tone in BP sounds like a minor third in 12-tone. The fact that a whole-tone sounds like a standard minor third is why we hear minor 7th chords all over the place in BP music. Don't worry if you don't know what any of that means!]
Remember how I said above that tritaves were hard to hear as the frame of the tuning? I'm convinced now that it may not be the case for anyone born and raised listening to the Bohlen-Pierce Scale or even anyone who intensely composes tonal Bohlen-Pierce Scale music over a long period. I say tonal because avant-garde or otherwise atonal music will not train your ear to hear the tritave as the frame. The tonality of organized chords and melodies will eventually coax our neurons to form the new connections we need to perceive the tritave as taking on the function of an octave.
Our neurons do what?
Our brains naturally have dynamical attractors (cooperating neurons) that pull on us when music lands on octaves, and other harmonic intervals to a lesser degree, to give us a feeling of stability and resolution. Whether musically trained or not, humans are wired to hear the octave as the main frame of reference. But if we deprive ourselves of octaves and instead immerse ourselves in an alien tuning that is not only devoid of octaves but also musically uses a different frame, our brains will eventually compensate.
One day, after immersing myself in tonal Bohlen-Pierce Scale music for many years, I heard the tritave as an octave, which scared me! It didn't just take on the function of an octave–it sounded like an octave. I thought I must be overly tired. But this has happened several times since then. Nowadays, almost every time I compose a new song in BP, I experience this phenomenon. I'll ask myself, "How did an octave sneak into the music?" thinking my synths need to be re-tuned. And then I realize, "Oh wow, that's a tritave! BP has broken my brain!" I go through this ridiculous thought process every time. It's as if my subconscious brain has grown new connections, but my aware brain is still uncomfortable with it. So, each time now, I'll take a moment to hear the tritave as its own interval while embracing its function as the frame.
Don't worry. You won't lose your ability to hear an octave as the frame in other tunings! That's a hard wiring.
One conclusion I've made is that it must be more critical that there IS a frame and less important as to what it is. Listen to tonal Bohlen-Pierce Scale music long enough, and you may someday hear the tritave act like an octave. It's an extraordinary feeling.
Research
I wrote this research paper on the Bohlen-Pierce Scale for an Advanced Acoustics class at New York University in the Spring of 2001 while obtaining my master's degree in Music Technology. It included listening tests with nine subjects with a wide range of musical training. Some were beginners, and some were long-time professional musicians. Many people think this was my master's thesis, but it was just a final project in Acoustics class, where we could pick a topic as long as the teacher approved it. I saw it as an opportunity to learn more about the Bohlen-Pierce Scale, so I asked my teacher if I could write about the "acoustics" of the Bohlen-Pierce Scale, and they were okay with that. :D The fact is, I found myself torn between choosing the Bohlen-Pierce Scale or Chaos Melody Theory as my master's thesis, and ended up choosing the latter since it was more of my own creation.Here is the main Bohlen-Pierce Scale website, formerly run by Heinz Bohlen.
Bohlen-Pierce Modes and Tunings
Modes and Chords

Some modes and chords are mapped out here, which you may find useful.
I will always cherish this image from the website. It's the Lambda family wheel that Heinz Bohlen drew in 2001. Read the fun story about it here.

Listen to Bohlen-Pierce Scale music
Go here for a full playlist.Elaine Walker
Involution | Involution YouTube (2023, Elaine Walker / No Terrestrial Road)
Magic Rectangle (2021, Elaine Walker / Four-Momentum)
Infinity | Infinity video performance (2019, Elaine Walker / Four-Momentum)
Euler's Identity (2018, Elaine Walker / Four-Momentum)
Love Song | Love Song live performance at Berklee | Love Song YouTube (2011, ZIA / Drum'n'Space)
Greater Good | Greater Good practicing at home | Greater Good YouTube (2011, ZIA / Drum'n'Space)
1-rx^2 Part1 | Part2 | Part3 | Part4 (1992, composed in MAX using Chaos Melody Theory)
Agribusiness (1992, ZIA / v1.5)
Stick Men | Stick Men live performance at Berklee (1992, ZIA / v1.5)
Dr. Richard Boulanger
I Know of No Geometry
Solemn Song for Evening (live performance at the Bohlen-Pierce Symposium 2010)
Sevish
Orbital (Bohlen-Pierce beat)
Mashroon (microtonal drum & bass, Bohlen Pierce scale)
Find more music on the main Bohlen-Pierce Scale website.
Other videos
Bohlen-Pierce Scale Symposium, Boston 2010: Videos of Performances and LecturesMy lecture at the Bohlen-Pierce Scale Symposium, Boston 2010: 5 Videos
AXIS keyboard for the Bohlen-Pierce Scale: 11 Videos
Building a Bohlen-Pierce Scale Vertical Keyboard: 1 Video
Hearing Inversions in BP – Listening Examples: 4 Videos
Keyboards


Bohlen-Pierce keyboards are discussed here, as well as featured in the above videos.
The Inventors of the Bohlen-Pierce Scale

Heinz Bohlen at Stanford, 1935–2016
(Picture by Elaine Walker, 2001)

John Robinson Pierce, 1910–2002
(Picture courtesy of CCRMA, Stanford, CA)
There is a lot of history that you can read here. What follows is my experience, including what Heinz Bohlen told me directly about the history of the scale.
The story of the Bohlen-Pierce Scale and its inventors is a bittersweet one. Sadly, the two microwave engineers who invented the scale independently six years apart never met, even though they both lived in the San Francisco area for a number of years. When John Pierce passed away in 2002, Heinz's dream of meeting him and discussing their co-invented scale in person died with him. Heinz was also a fan of John Pierce because of his microwave engineering fame. John Pierce invented the idea of the communication satellite and coined the word transistor. In turn, John Pierce may have been envious that Heinz Bohlen invented the Bohlen-Pierce Scale six years before he did.
It all started in the early 1970s when Heinz Bohlen became curious about why musicians always use the 12 notes per octave tuning. After getting some unsatisfactory answers from musicians, he took it upon himself to research music and tonality. Finally, the understanding of combination tones led him to believe he could use the same method that led to the 12-tone equal temperament to devise another tuning from a different framework. Heinz understood that the 12-tone scale was based on the major triad and its inversion, and then the gaps were filled in to create the 12 notes. So, he started with a new triad that was very harmonically pure but not contained within the standard 12-tone framework. Heinz made the stunning discovery that a scale of thirteen almost equal steps within the framework of an octave and a fifth (which John Pierce later dubbed as a tritave) contained this pure triad. He recognized that this tuning shared a duality with the traditional Western 12-tone tuning; it had harmonic value and could be a valid compositional tool.
Amazingly, during the same time frame, Kees van Prooijen had independently invented the BP Scale during his research in generic equal temperaments. But even more surprising, a second microwave engineer named John R. Pierce made the same discovery six years later. He arrived at the tuning using a different method, but for the same reason – Curiosity. Leave it to microwave engineers to invent a tuning with no octaves! When John Pierce realized Heinz Bohlen had already invented it, the tuning was dubbed the "Bohlen-Pierce Scale. Both were unaware of Kees van Proojijen.
And there is another super-coincidence – John Pierce wrote "The Science of Musical Sound," my favorite childhood coffee table book. I realized the connection sometime after my professor at Berklee College of Music, Dr. Boulanger, introduced me to the "Pierce Scale" in 1991. I knew John R. Pierce sounded familiar, but I couldn't think why. I saw the book on my parents' coffee table that Christmas, then realized why John R. Pierce's name sounded so familiar! I remembered how much I had loved the book when I was younger. It has pictures of audio waveforms and harmonics, which was eye-opening to the younger me who hadn't encountered any of those topics yet.
I had the pleasure of meeting Heinz Bohlen in 2001 in San Jose, where he lived, when I was on a trip to visit Stanford. We both ventured to Stanford looking for Max Mathews (the "Father of computer music"), but he was not there that week. We hoped to have a grand reunion of Max Mathews, John Pierce, Heinz Bohlen, and myself. Dr. Richard Boulanger ("Dr. B") has also worked extensively with Max Mathews and John Pierce on Bohlen-Pierce Scale music and research. Dr. B informed me that John Pierce was in the hospital with Alzheimer's and was not taking visitors. Alas, the reunion never happened, but I found Heinz Bohlen to be delightful company over sushi. He took a great interest in my Chaos Melody Theory research, and we pondered about chaos theory more than the BP Scale! Heinz and I kept in touch and remained friends ever since.
John R. Pierce passed away the following year. Heinz passed away in 2016. I had email communications with him over the years since then, when he was living in Germany, but I only got to see him once over video at the Bohlen-Pierce Scale Symposium in Boston in 2010. I got to say hi during the question and answer session. It hit me quite hard hearing of his passing. I had just moved to my childhood home to care for my parents, and Mom was Heinz's age, also born in 1935.
– EW

Heinz and Elaine at Stanford, 2001

The Science of Musical Sound was my favorite childhood "coffee table" book. It's a coincidence. No joke!