The conic geometry of rectangles inscribed in lines, Proc. Amer. Math. Soc. 149 (2021), 2625-2638
Authors: Bruce Olberding, Elaine A. Walker
Abstract: We develop a circle of ideas involving pairs of lines in the plane, intersections of hyperbolically rotated elliptical cones and the locus of the centers of rectangles inscribed in lines in the plane. Submitted 2 August, 2021; v1 submitted 15 August, 2019; originally announced August 2019.
Authors: Bruce Olberding, Elaine A. Walker
Abstract: We develop a circle of ideas involving pairs of lines in the plane, intersections of hyperbolically rotated elliptical cones and the locus of the centers of rectangles inscribed in lines in the plane. Submitted 2 August, 2021; v1 submitted 15 August, 2019; originally announced August 2019.
The following figure shows a configuration of four lines A,B,C,D and the cones generated by the pairs A,C and B,D, with the red intersection of two HR-cones (hyperbolically rotated cones) projected vertically onto the x,y plane. The red hyperbola in the plane consists of the center points of all rectangles inscribed in sequence in the configuration A,B,C,D.

The following two figures show an intersection of two HR-cones. The red curve is the intersection of the two cones. In the 2nd figure the cones have been removed to show the space curve that is the intersection of the two cones.

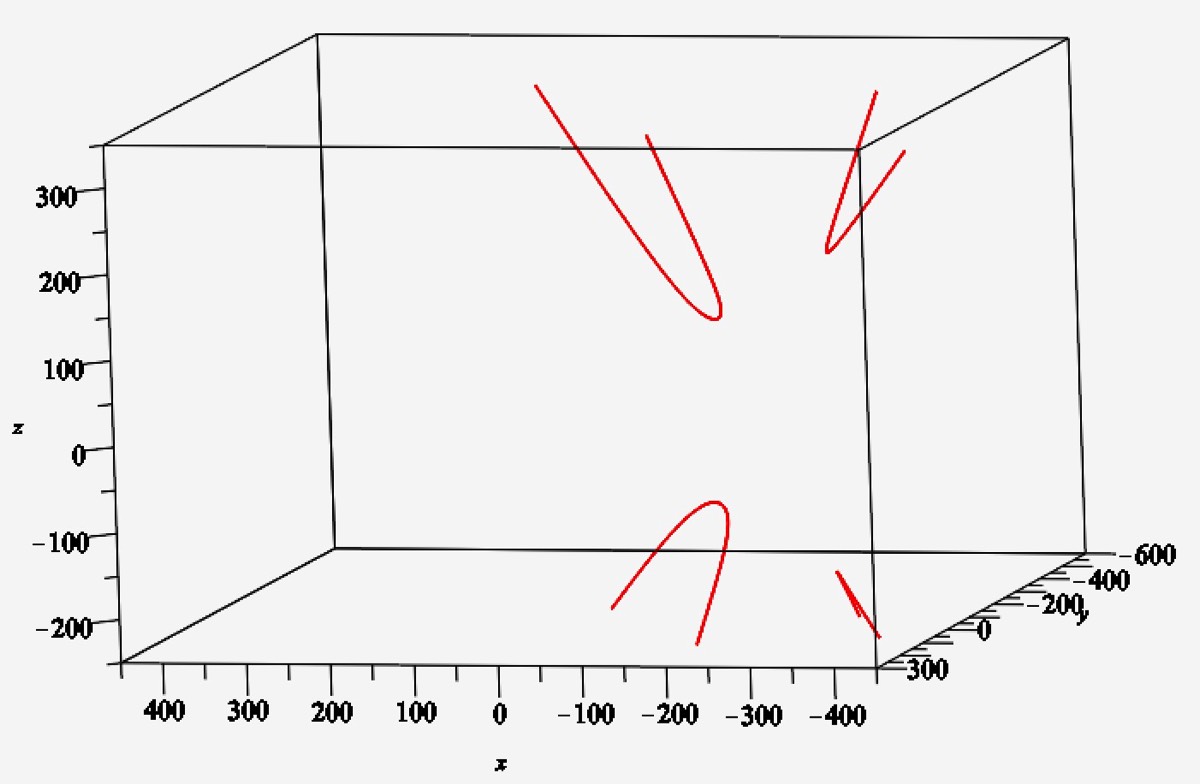
The following video shows different views of the space curve in the above graphs. At 2 seconds, it is clear that the upper left branch does not lie in a plane. (See Remark 4.12.) The video ends with a view directly from above the cones, which shows the projection of the space curve to the xy-plane. This hyperbola in the plane is the rectangle locus for the two pairs of lines (not shown) that are comprised of the generating lines for the two cones.
This illustrates how we generate the cones.
The space-time graph on the left shows a level curve at height 1 of an HR cone and the generating lines of the HR cone.
A pair of orthogonal lines generates a round cone, illustrated as the unit circle on the graph. Round cones have interesting properties such as retaining no information about the rotation of their orthogonal line pair. Rotating an orthogonal line pair of a quadrilateral will have no effect on the quadrilateral's rectangle locus. Think of how rotating a round cone will not change its intersection with another cone.
Lines A and B in the graph generate a hyperbolically rotated (Lorentz-squeezed) cone. The cone ellipse touches the same hyperbola level as the unit circle. Intersecting with the unit circle locates the cone lines as in Remark 3.7. The graph on the right illustrates the effect of a hyperbolic rotation, showing how points along the unit circle are "rotated" along the hyperbolas in the family of hyperbolas having asymptotes y = x and y = -x.
We give round cones 45 degree sides, and any other cones are 45 degrees, vertically above the lines.
The space-time graph on the left shows a level curve at height 1 of an HR cone and the generating lines of the HR cone.
A pair of orthogonal lines generates a round cone, illustrated as the unit circle on the graph. Round cones have interesting properties such as retaining no information about the rotation of their orthogonal line pair. Rotating an orthogonal line pair of a quadrilateral will have no effect on the quadrilateral's rectangle locus. Think of how rotating a round cone will not change its intersection with another cone.
Lines A and B in the graph generate a hyperbolically rotated (Lorentz-squeezed) cone. The cone ellipse touches the same hyperbola level as the unit circle. Intersecting with the unit circle locates the cone lines as in Remark 3.7. The graph on the right illustrates the effect of a hyperbolic rotation, showing how points along the unit circle are "rotated" along the hyperbolas in the family of hyperbolas having asymptotes y = x and y = -x.
We give round cones 45 degree sides, and any other cones are 45 degrees, vertically above the lines.


The next video illustrates a flow of rectangles along the rectangle locus of a configuration of four lines A,B,C,D. The flow is parameterized by slope of the rectangle side having vertices on A and B. The asymptotes and lines of symmetry for the rectangle locus are shown as well.
The next video illustrates a flow of rectangles along the rectangle locus of a configuration of four lines A,B,C,D. Two rectangles are shown at a time, so the locus is traced over twice. The flow is parameterized by slope of the rectangle side having vertices on A and B. The lines of symmetry for the rectangle locus are shown as well.
The following video illustrates the rectangle flow, with traces, on a configuration of four lines A,B,C,D. The rectangle sides are extended and colored to show a spiraling effect.
The video below illustrates the rectangle flow on a configuration with parallel lines. The locus appears as a double line with a gap, however there is only one rectangle associated with the two boundary points and two rectangles per point along the rest of the locus. In a second paper [see the article Paths of rectangles inscribed in lines over fields] we show this locus is the image of a hyperbola under an affine transformation.
The following video illustrates how the rectangle locus changes as one line in the configuration is rotated. When the blue lines merge, the cone is flattened. For more on this last phenomenon, see [the article Paths of rectangles inscribed in lines over fields].
The following video illustrates how the rectangle locus changes as one line is translated in the configuration. The diagonals of the underlying quadrilateral are shown as well. When these diagonals are perpendicular, the locus is a degenerate hyperbola. For more on this last phenomenon, see [the article Paths of rectangles inscribed in lines over fields].
The following video illustrates how the rectangle locus changes as two lines are translated in the configuration. At the end of the video the hyperbola flattens. In a second paper [see the article Paths of rectangles inscribed in lines over fields] we show this locus, when completely flattened, is the image of a hyperbola under an affine transformation.
The next video illustrates the same motion as the video above, but showing the cone intersections overlaid.
The next video illustrates how the intersection of a pair of HR-cones changes as the defining pairs of lines are translated so that only the positions of the cones are changed.
The video below illustrates Theorem 5.3. The position and shape of these HR-cones are dictated by the semialgebraic surface in the proof of the theorem and show how different pairs of HR-cones can produce the same hyperbola as a projection of the intersection of the two cones to the plane. This hyperbola would be, as in Corollary 5.4, the rectangle locus for two pairs of lines, namely the pairs comprised of the generating lines of the cones.
This series of examples illustrates the rectangle loci for different pairings of four lines A, B, C, D. The rectangle loci are found as in Lemma 4.3 by intersecting the HR-cones generated by the different pairings. For example, the first snapshot involves the intersection of the HR-cones generated by the pairs AB and CD. The snapshot is taken from above, looking directly down into the two HR-cones. (The two cones are only shown below a fixed height.) The four lines are superimposed on the cross-section in order that their relationship to the two cones is more apparent. The small spheres mark the center of the cone of corresponding color as well as the paired lines that determine the cone. By Lemma 4.3, the projection to the xy-plane of the intersection of the cones is the rectangle locus for the two pairs. In the first three snapshots, this projection is a non-degenerate hyperbola.
