Bisector fields and projective duality, arXiv:2306.08612
Authors: Bruce Olberding, Elaine A. Walker
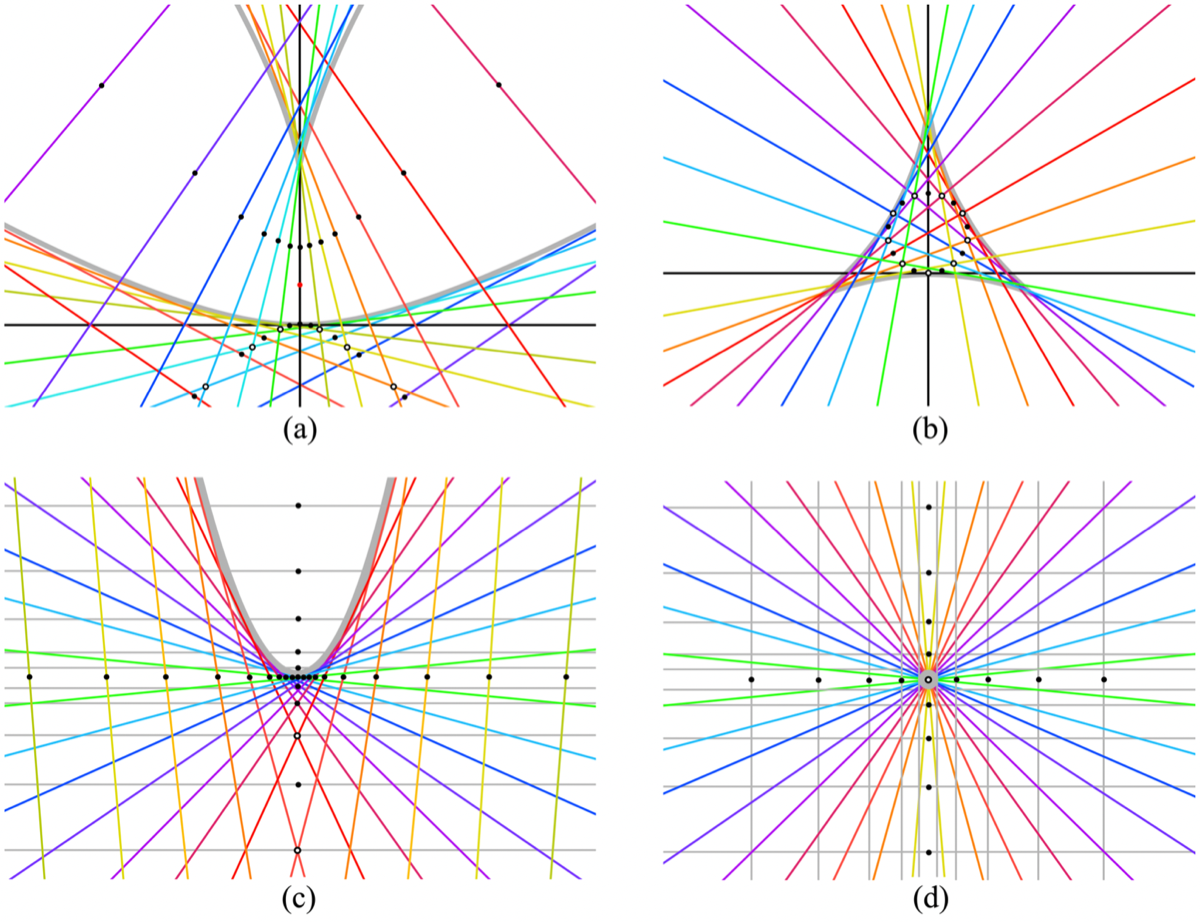
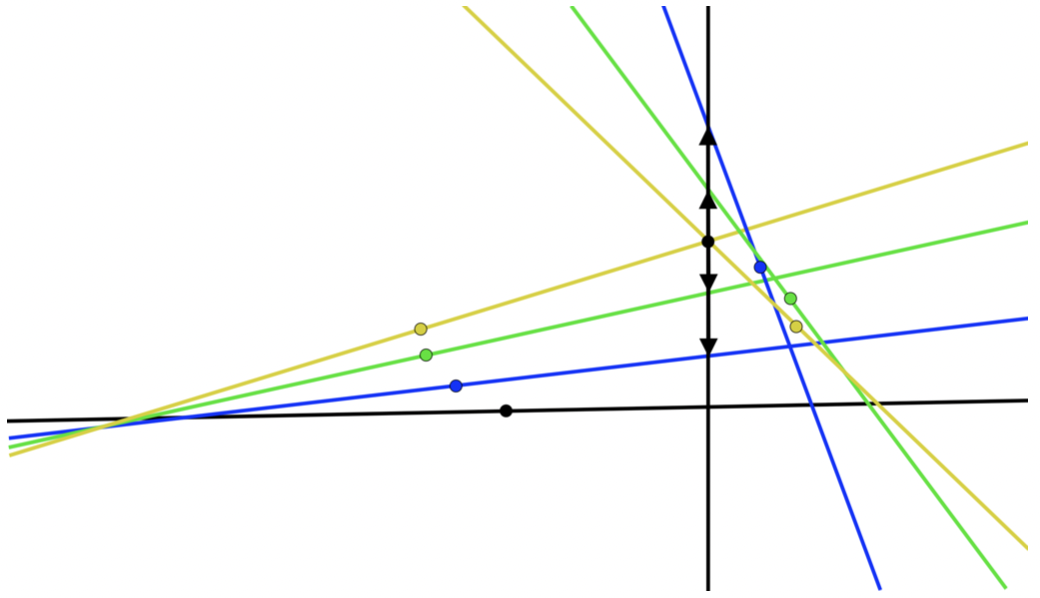
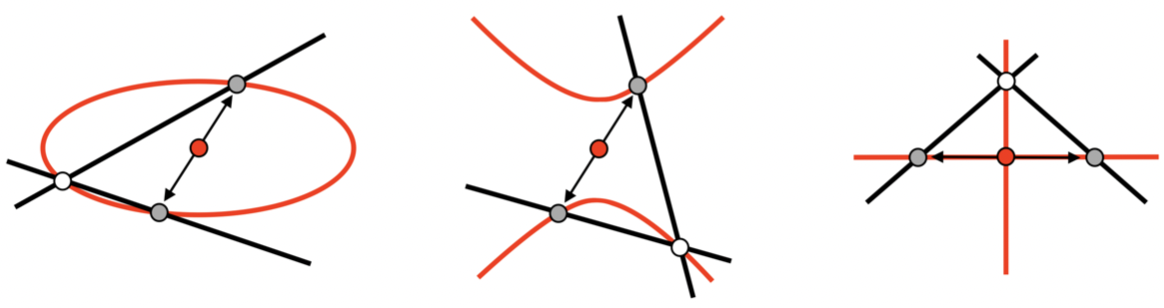
Abstract. Working over a field k of characteristic ≠ 2, we study what we call bisector fields, which are arrangements of paired lines in the plane that have the property that each line in the arrangement crosses the paired lines in pairs of points that all share the same midpoint. To do so, we use tools from the theory of algebraic curves and projective duality. We obtain a complete classification if k is real closed or algebraically closed, and we obtain a partial classification if k is a finite field. A classification for other fields remains an open question. Ultimately this is a question regarding affine equivalence within a system of certain rational quartic curves.
Submitted 14 June, 2023; originally announced June 2023.
Authors: Bruce Olberding, Elaine A. Walker
Abstract. Working over a field k of characteristic ≠ 2, we study what we call bisector fields, which are arrangements of paired lines in the plane that have the property that each line in the arrangement crosses the paired lines in pairs of points that all share the same midpoint. To do so, we use tools from the theory of algebraic curves and projective duality. We obtain a complete classification if k is real closed or algebraically closed, and we obtain a partial classification if k is a finite field. A classification for other fields remains an open question. Ultimately this is a question regarding affine equivalence within a system of certain rational quartic curves.
Submitted 14 June, 2023; originally announced June 2023.
Read the [pdf].