Bisector fields and pencils of conics, arXiv:2305.08324
Authors: Bruce Olberding, Elaine A. Walker
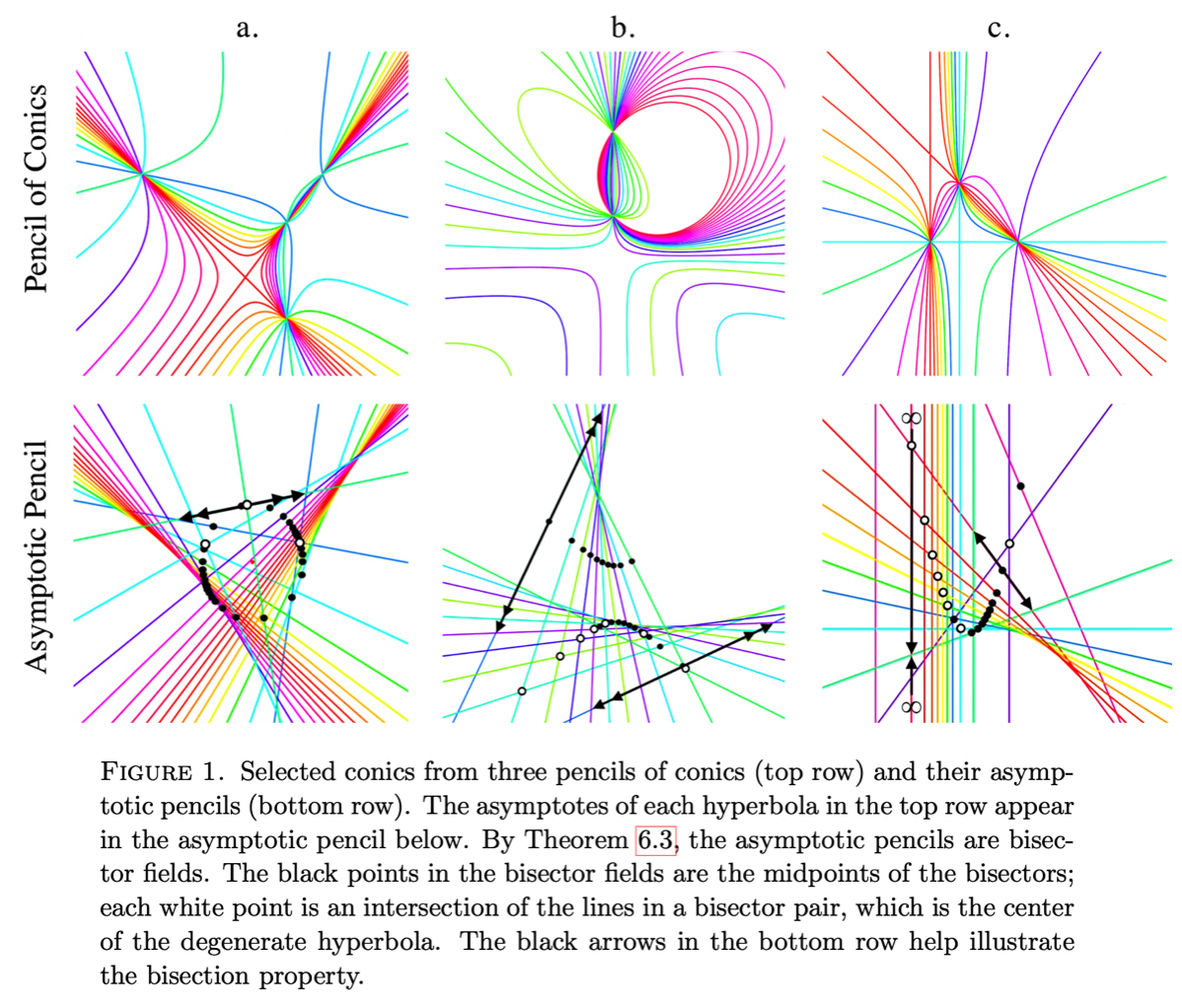
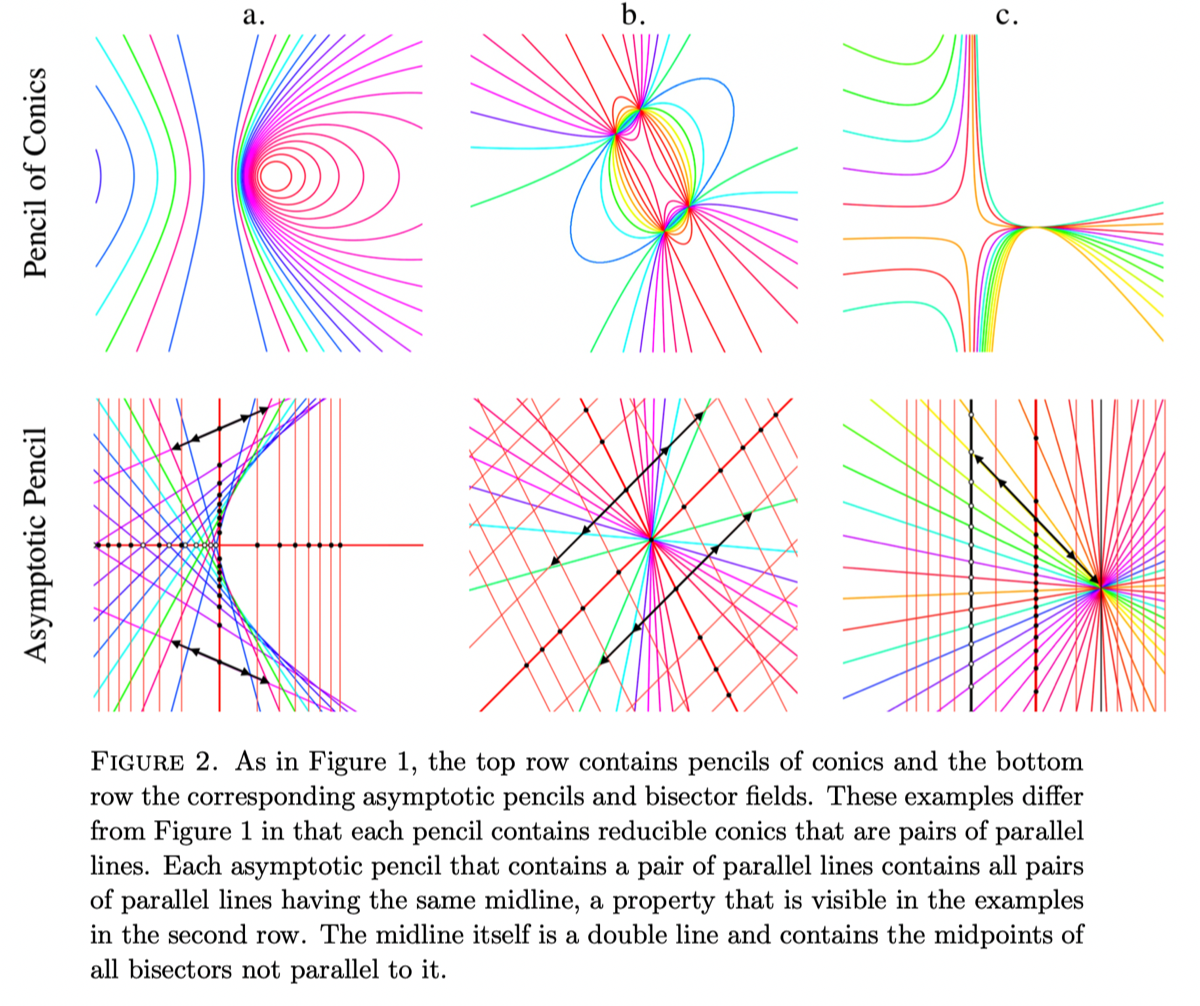
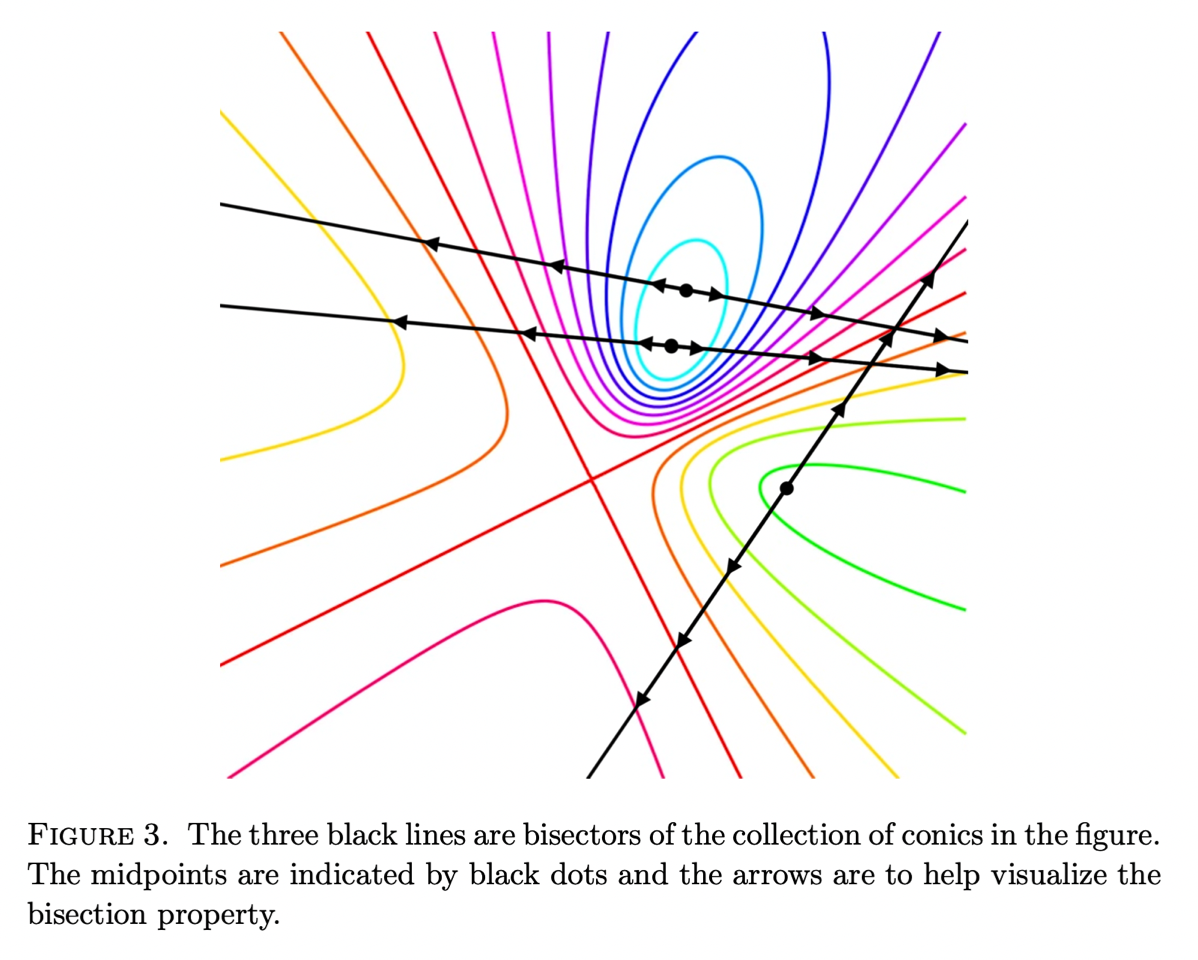
Abstract: Working over a field of characteristic other than 2, we show that the degenerations of the conics in a nontrivial pencil of affine conics form an arrangement of pairs of lines that we call a bisector field, a maximal set B of paired lines such that each line in B simultaneously bisects each pair in B. Conversely, every bisector field arises this way from a pencil of affine conics.
Submitted 14 May, 2023; originally announced May 2023
Authors: Bruce Olberding, Elaine A. Walker
Abstract: Working over a field of characteristic other than 2, we show that the degenerations of the conics in a nontrivial pencil of affine conics form an arrangement of pairs of lines that we call a bisector field, a maximal set B of paired lines such that each line in B simultaneously bisects each pair in B. Conversely, every bisector field arises this way from a pencil of affine conics.
Submitted 14 May, 2023; originally announced May 2023