Bisector fields of quadrilaterals, Contributions to Algebra and Geometry (2024)
Authors: Bruce Olberding, Elaine A. Walker
Abstract: Working over a field of characteristic other than 2, we examine a relationship between quadrilaterals and the pencil of conics passing through their vertices. Asymptotically, such a pencil of conics is what we call a bisector field, a set 𝔹 of paired lines such that each line ℓ in 𝔹 simultaneously bisects each pair in 𝔹 in the sense that ℓ crosses the pairs of lines in 𝔹 in pairs of points that all share the same midpoint. We show that a quadrilateral induces a geometry on the affine plane via an inner product, under which we examine pencils of conics and pairs of bisectors of a quadrilateral. We show also how bisectors give a new interpretation of some classically studied features of quadrangles, such as the nine-point conic. Submitted 19 May, 2023; originally announced May 2023.
Authors: Bruce Olberding, Elaine A. Walker
Abstract: Working over a field of characteristic other than 2, we examine a relationship between quadrilaterals and the pencil of conics passing through their vertices. Asymptotically, such a pencil of conics is what we call a bisector field, a set 𝔹 of paired lines such that each line ℓ in 𝔹 simultaneously bisects each pair in 𝔹 in the sense that ℓ crosses the pairs of lines in 𝔹 in pairs of points that all share the same midpoint. We show that a quadrilateral induces a geometry on the affine plane via an inner product, under which we examine pencils of conics and pairs of bisectors of a quadrilateral. We show also how bisectors give a new interpretation of some classically studied features of quadrangles, such as the nine-point conic. Submitted 19 May, 2023; originally announced May 2023.

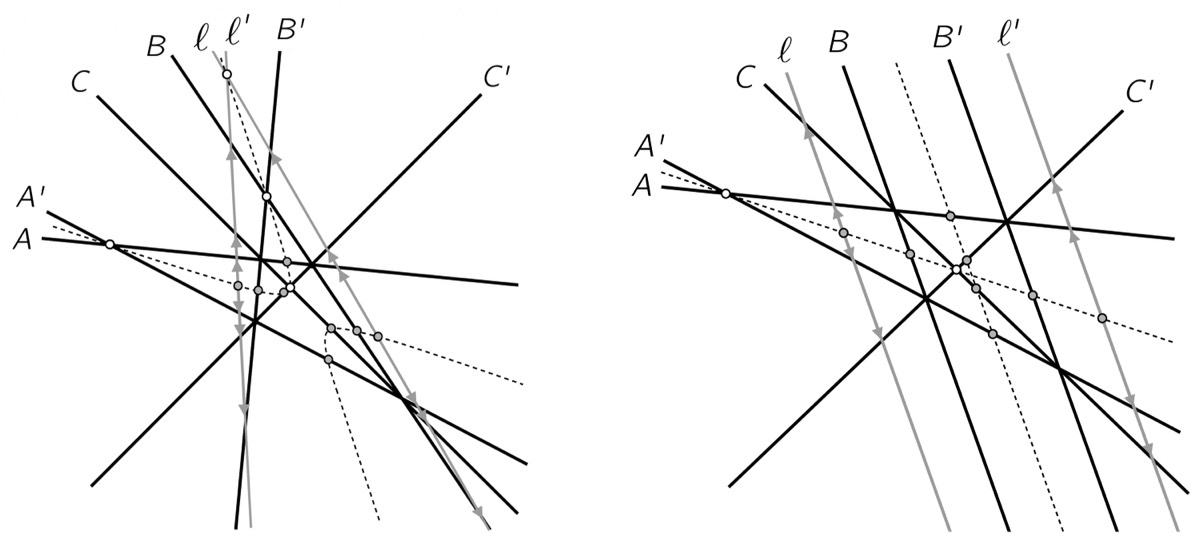
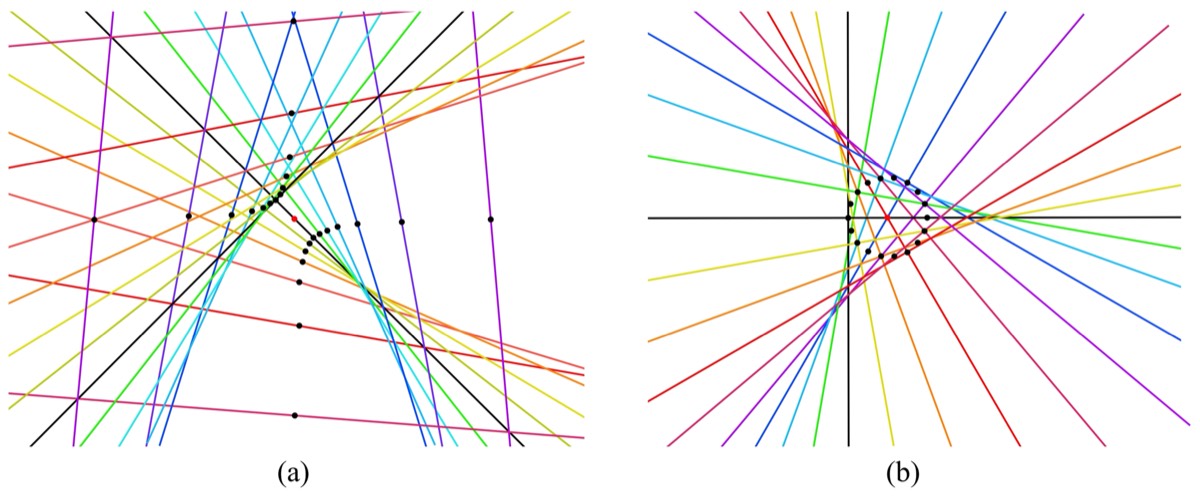
Figure 1. Selected pairs from a bisector field, with each pair indicated by color. The marked points trace out a hyperbola and are the midpoints of bisectors of the same color. Each bisector bisects all other pairs with respect to the same midpoint.
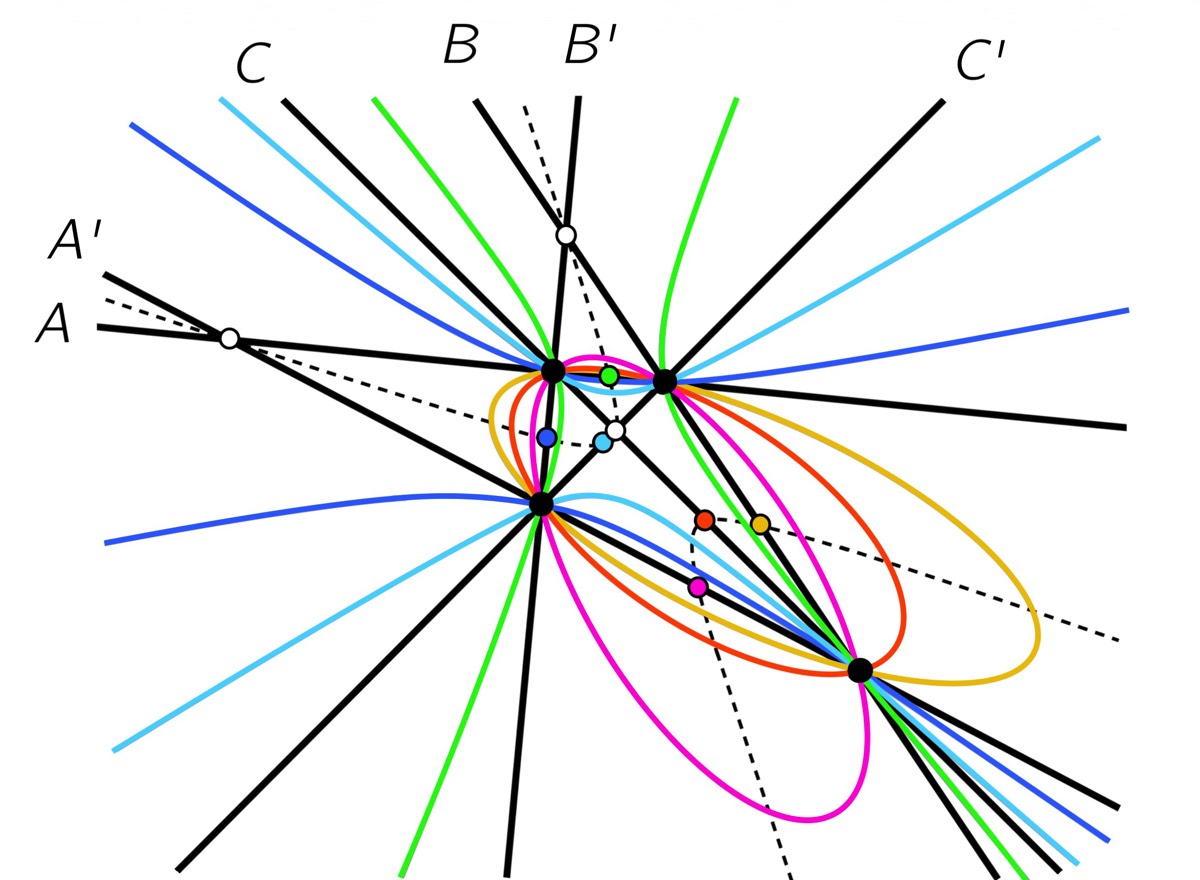
Figure 2. These nine conics (3 ellipses, 3 nondegenerate hyperbolas and 3 degen- erate hyperbolas) belong to the pencil of conics through the four black points. The nine conics are centered on the midpoints and diagonal points of the quadrilateral whose vertices are the four black points, and hence these centers are the nine dis- tinguished points that define the nine-point conic for this quadrilateral, which is the dotted hyperbola. The asymptotes of the hyperbolas in the pencil here are also bisector pairs in the bisector field of the quadrilateral.
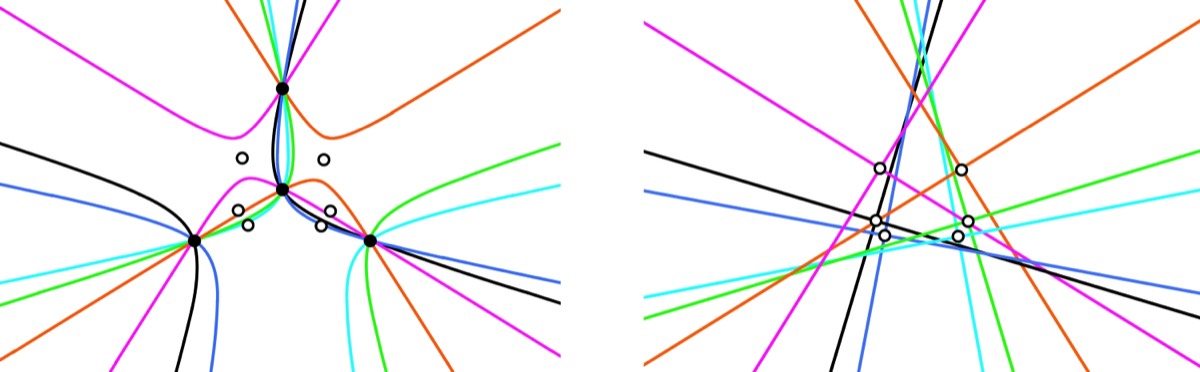
Figure 3. On the left are several conics belonging to the pencil through the four black points. The centers of these conics are marked with white points. On the right are the asymptotes of these same conics. The asymptotes of the black hyperbola at left are the black lines at right. By Theorem 6.4, these pairs belong to the bisector field of the quadrilateral defined by the pencil. The midpoints of the bisectors are the white points.
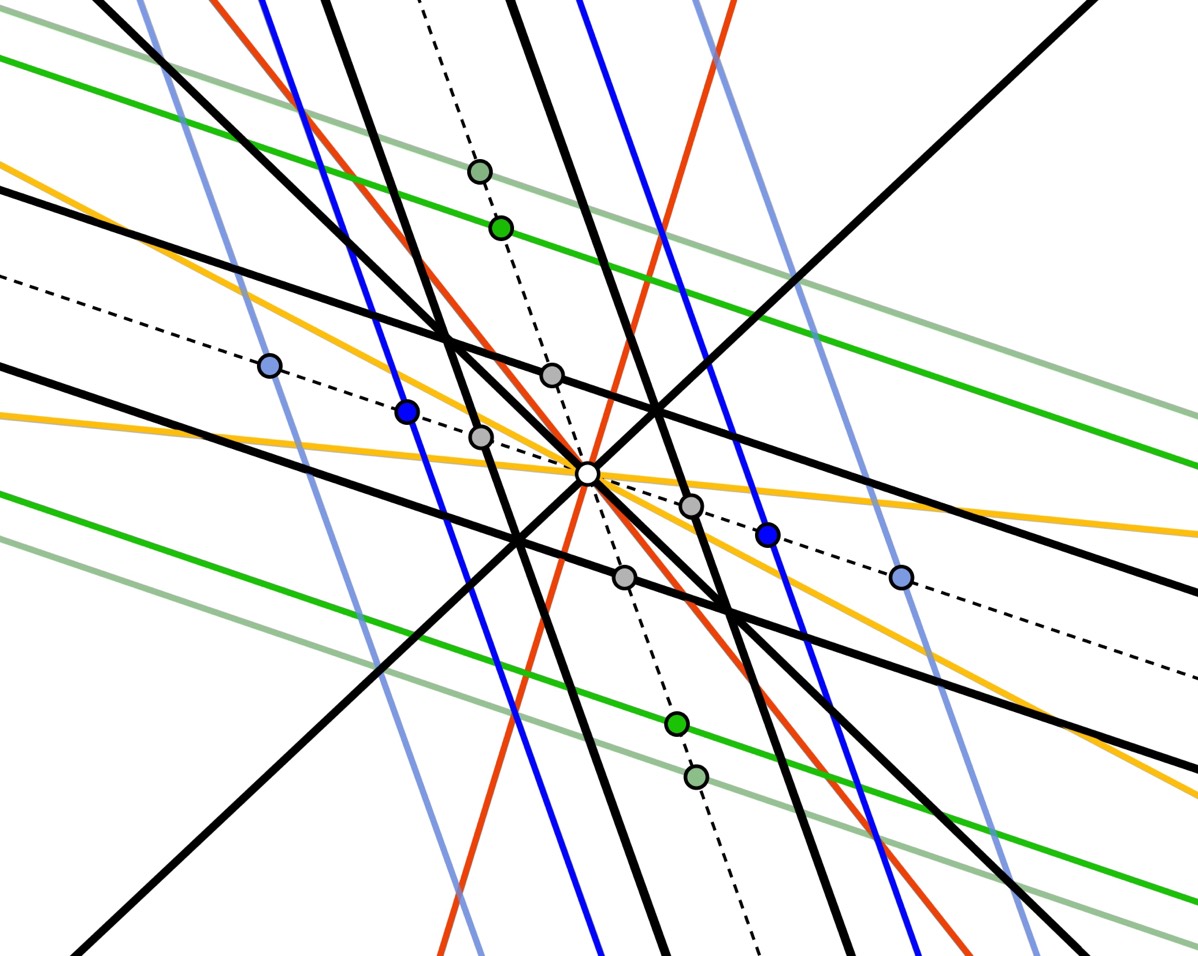
Figure 4. Pairs from a bisector field of a parallelogram. All the lines through the center point are bisectors having the center as their midpoint. The lines through the center are paired according to the shade of gray with which they are colored. The parallel lines are paired via antipodal midpoints.