Paths of rectangles inscribed in lines over fields, Beitr Algebra Geom (2022)
Authors: Bruce Olberding, Elaine A. Walker
Abstract: We study rectangles inscribed in lines in the plane by parametrizing these rectangles in two ways, one involving slope and the other aspect ratio. This produces two paths, one that finds rectangles with specified slope and the other rectangles with specified aspect ratio. We describe the geometry of these paths and its dependence on the choice of four lines. Our methods are algebraic and work over an arbitrary field. Submitted 16 December, 2020; v1 submitted 25 June, 2020; originally announced June 2020.
Authors: Bruce Olberding, Elaine A. Walker
Abstract: We study rectangles inscribed in lines in the plane by parametrizing these rectangles in two ways, one involving slope and the other aspect ratio. This produces two paths, one that finds rectangles with specified slope and the other rectangles with specified aspect ratio. We describe the geometry of these paths and its dependence on the choice of four lines. Our methods are algebraic and work over an arbitrary field. Submitted 16 December, 2020; v1 submitted 25 June, 2020; originally announced June 2020.
FIGURE 1. Two sets of rectangles inscribed in four lines. The hyperbola is the set of centers of the inscribed rectangles. The at that the hyperbola here is non-degenerate (because its diagonal are not orthogonal; see Theorem 7.1) implies that no two rectangles inscribed in this configuration have the same slope or the same aspect ratio (see Section 8).
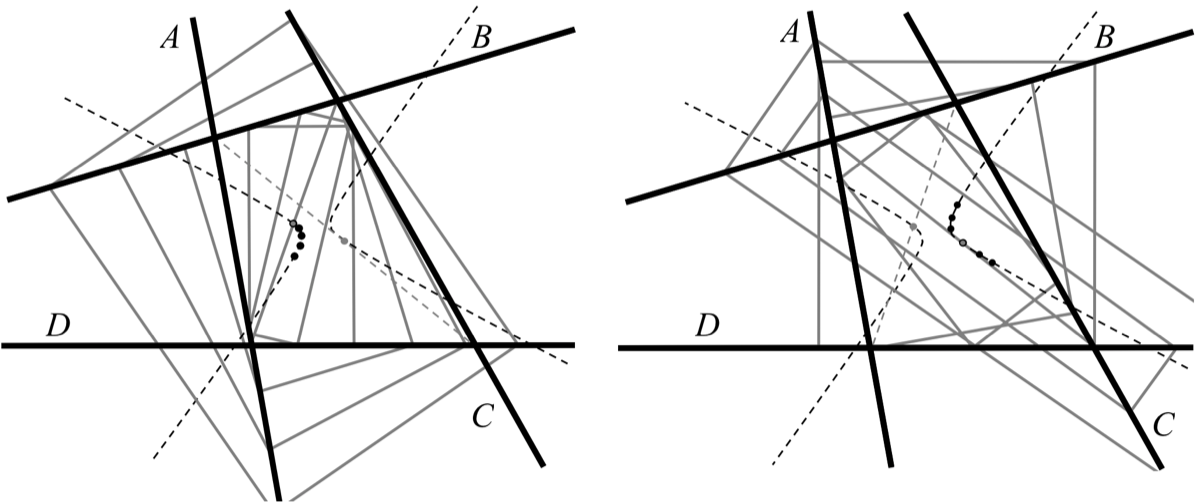
FIGURE 2. This configuration is degenerate because its diagonals are orthogonal (Theorem 7.1). The darker dotted line through each figure is a set of centers of inscribed rectangles. In the first figure, slope remains constant while aspect ratio changes, and in the second aspect ratio remains constant while slope changes. This phenomenon only happens in the degenerate case; compare to Figure 1. The centers of the rectangles in the first figure lie on the Gauss-Newton line through the midpoints of the diagonals, and in the second the centers lie on a line that is parallel to the diagonal through the intersection of A and C and that of B and D Theorem 9.1).
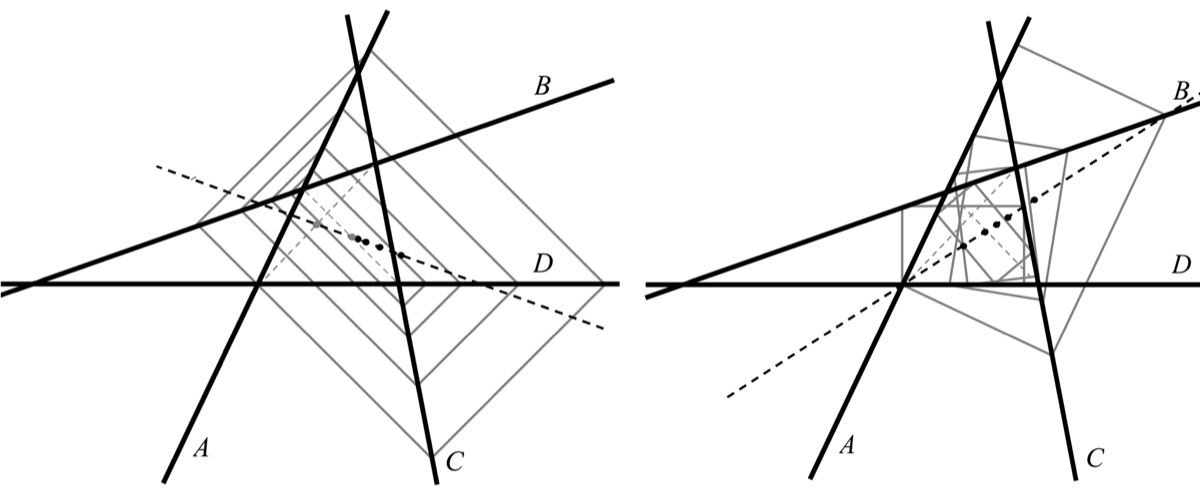
FIGURE 3. Three complete quadrilaterals ABCD and their diagonals E and F. The circles mark the pairs A, C and B, D that determine the configuration for each complete quadrilateral. Since none of the lines are parallel, each configuration determines a different quadrilateral (shaded gray) whose sides lie in sequence on A, B, C, D.
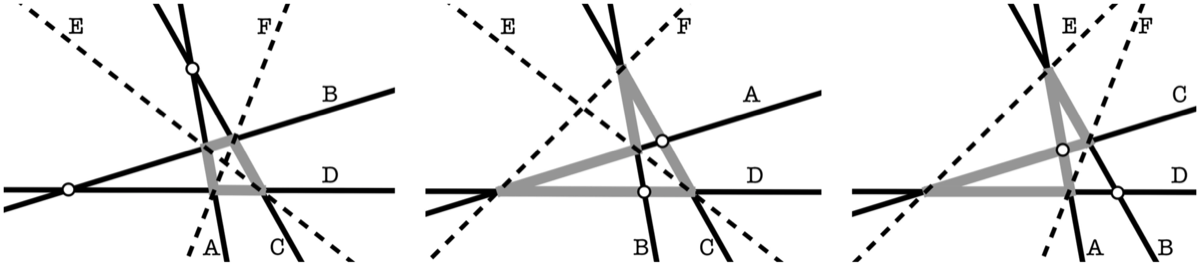
FIGURE 4. The diagonals of three complete quadrilaterals BCD with at least one set of parallel lines. In the second figure, the lines A and B are equal and so F is this same line also. In the third figure, the diagonal F is the line at infinity since the diagonal passes through the intersection of A and D and the intersection of B and C.
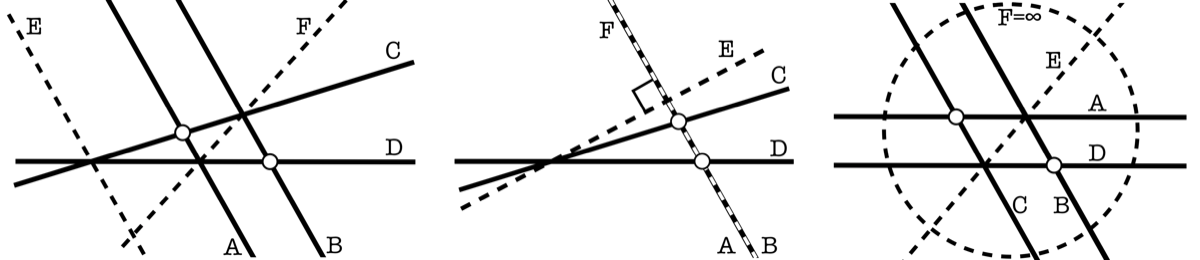

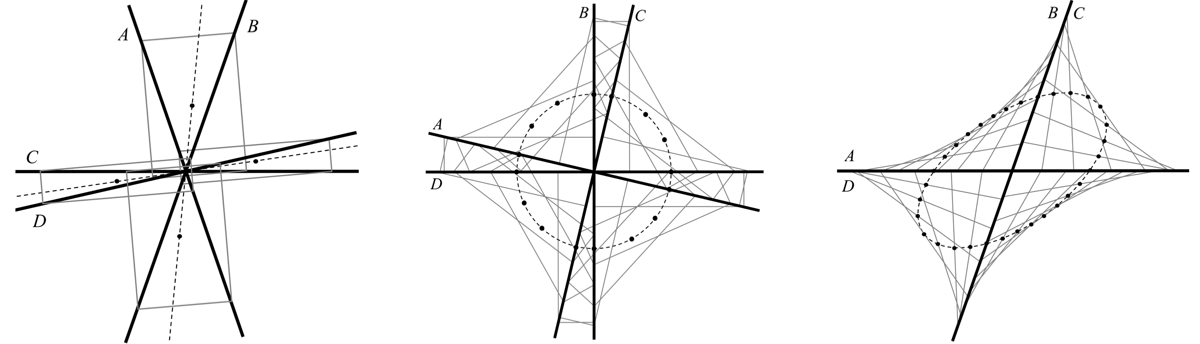
FIGURE 6. Rectangles inscribed in a configuration in which A = B. The set of centers of the rectangles on the aspect path is the slanted dotted line. All the rectangles this line have the same slope but never the same aspect ratio. The set of centers of the rectangles on the slope path is the horizontal dotted line. The rectangles along this line are all degenerate with aspect ratio 0 but none of the same slope. The aspect path of centers goes through the midpoint of the altitude of the visible triangle and the midpoint of its base, since these are the two diagonals of the configuration. See Theorem 9.1.
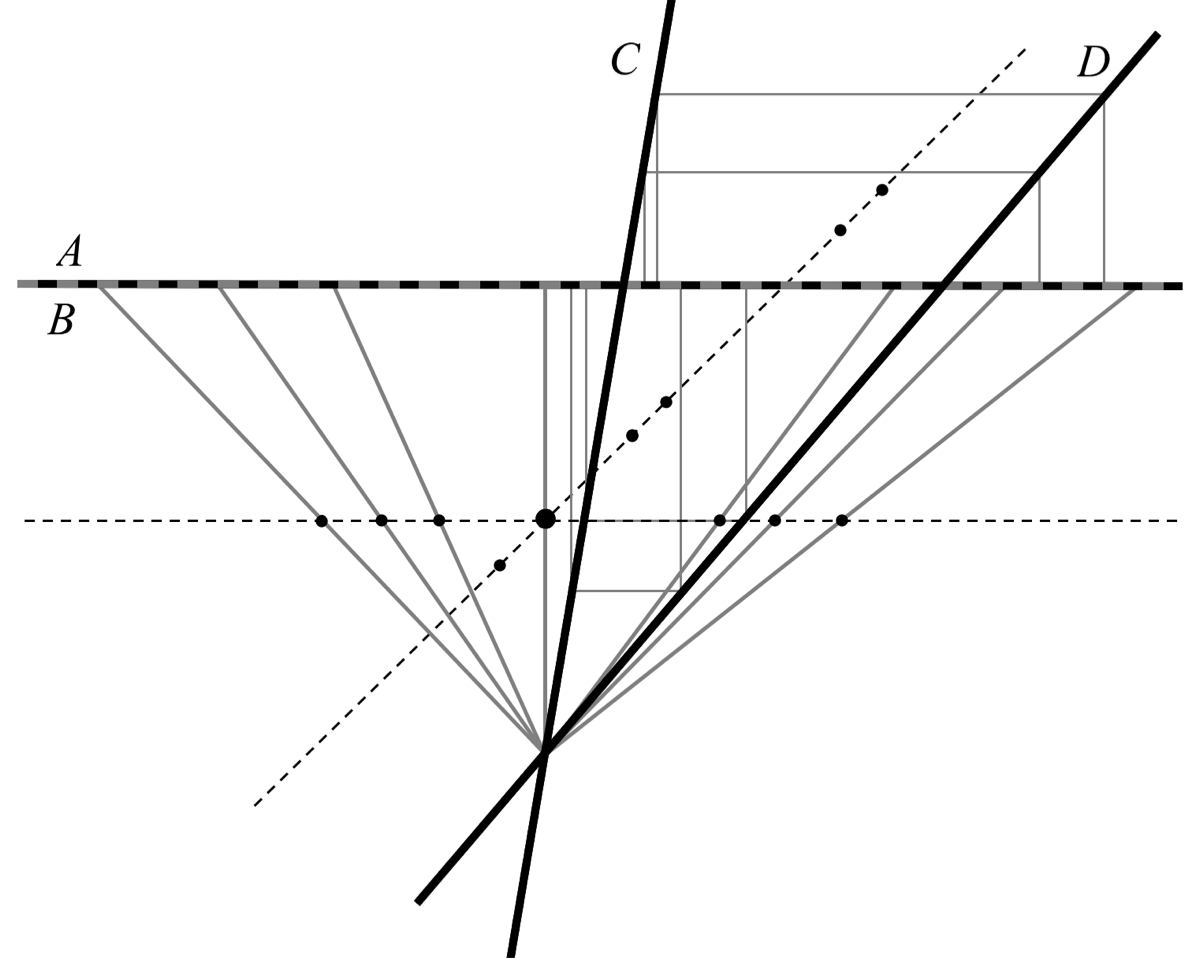
FIGURE 7. Rectangles inscribed in a configuration in which A, B and D are parallel. The rectangle locus, the dotted line in the figure, is a line with a gap. The configuration is non-degenerate, and so no two rectangles have the same slope or the same aspect ratio (see Theorem 7.1). Each point on the locus except the endpoints is the center of two inscribed rectangles. At the endpoints, there sonly one inscribed rectangle. This behavior is explained by the fact that the locus is the image of a hyperbola under an affine transformation.
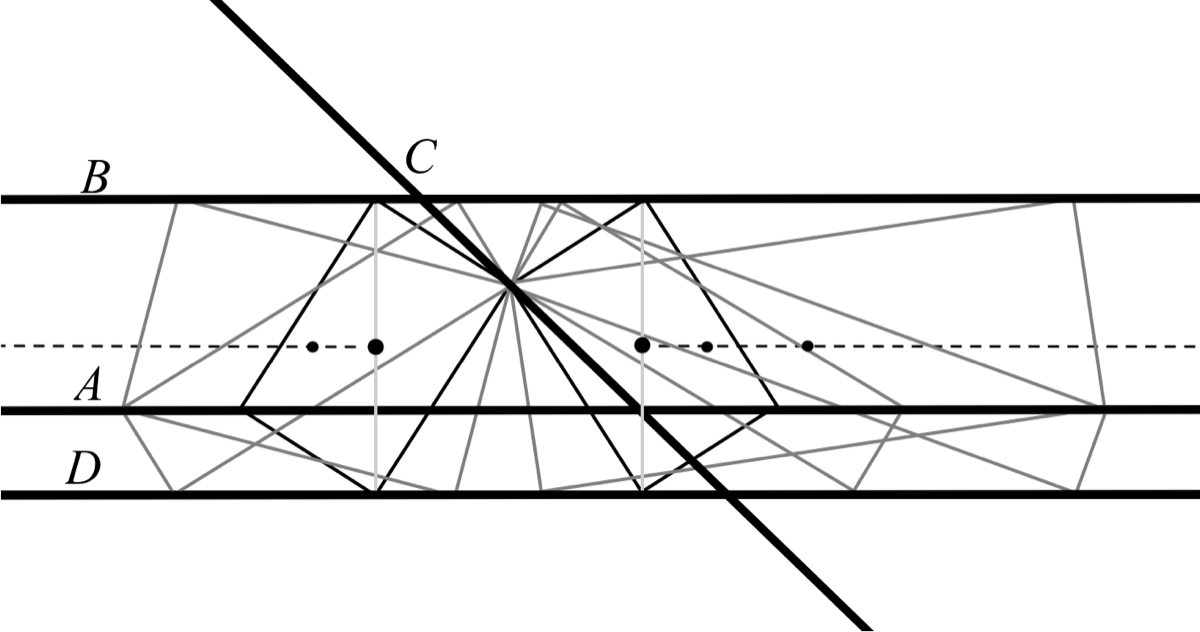
FIGURE 8. Rectangles inscribed in a configuration for which A || C and B || D. This configuration is nondegenerate because the diagonals E and F are not orthogonal; see Theorem 7.1. All rectangles share the same center, and so the rectangle locus is a single point. This point is the image of the planar hyperbola of rectangles in C under a linear transformation.
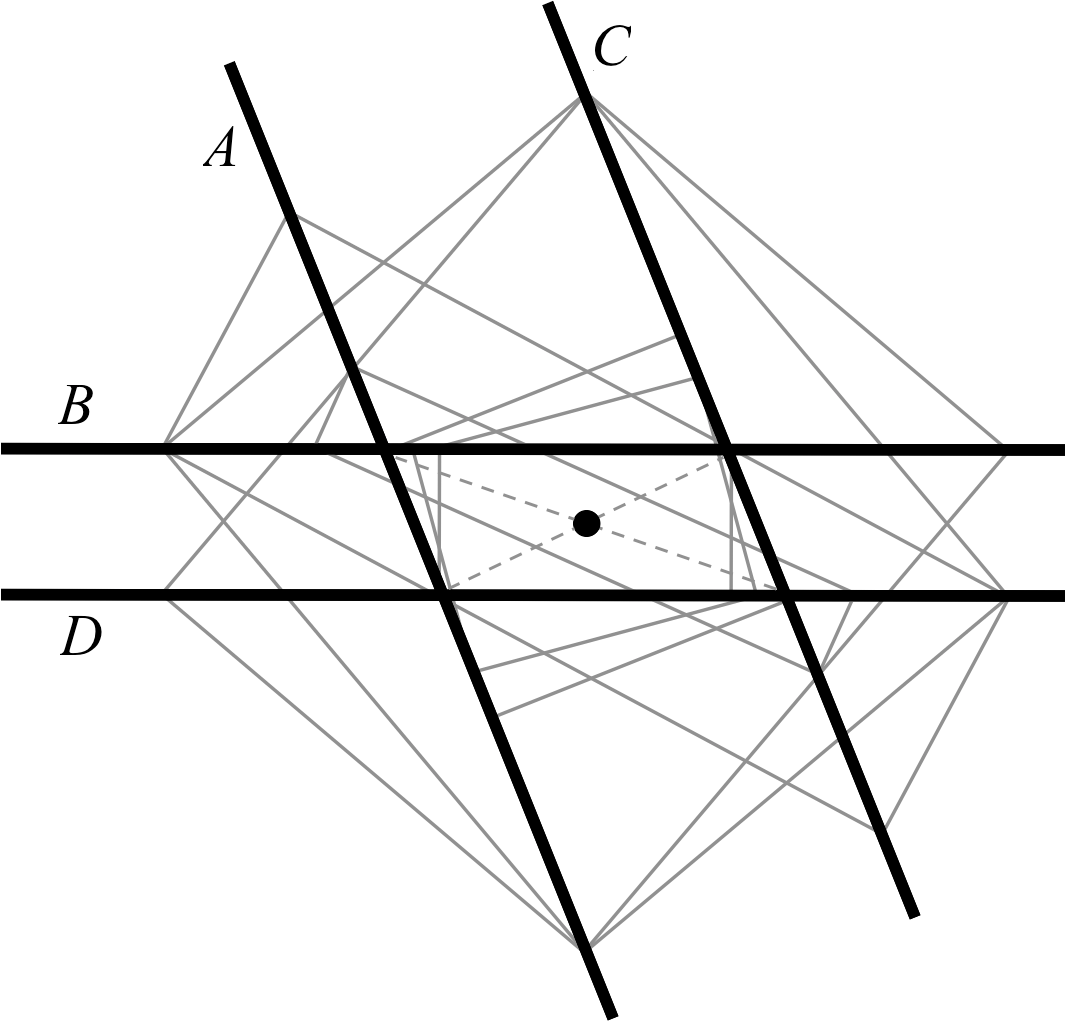
FIGURE 9. The first figure shows the centroid and center rectangles (wide and narrow, respectively). The rectangles at infinity are shown in the fourth figure. The rectangle at infinity for the slope path is the center rectangle with a quarter turn, while the rectangle at infinity for the aspect path is the centroid rectangle with a flip. The middle two images illustrate the turn and flip. In the first figure the aspect path of centers is the Gauss-Newton line and the slope path is parallel to the diagonal G (see Theorem 9.1).
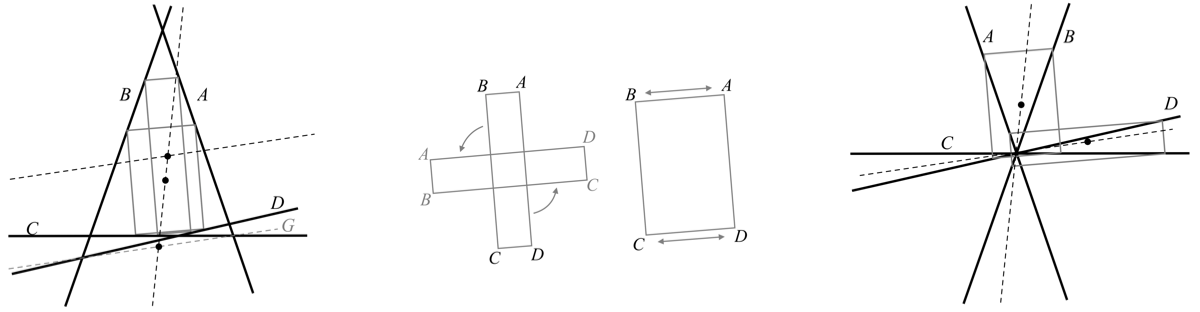
FIGURE 10. Rectangles inscribed in a configuration in which all four lines are parallel. The rectangles are centered on the dotted line, which infinitely many rectangles centered on each such point. Every point on the locus is the center of 4 rectangles having a fixed diagonal length, except when a diagonal is orthogonal to the four lines, in which case there are only 2 rectangles.
The following video illustrates how the rectangle locus changes as one line in the configuration is rotated. The locus moves through degenerate and non-degenerate configurations. When the blue lines merge, it is the image of a hyperbola under an affine transformation.
The following video illustrates how the rectangle locus changes as one line is translated in the configuration. The diagonals of the underlying quadrilateral are shown as well. When these diagonals are perpendicular, the locus is a degenerate hyperbola.
The following video illustrates how the rectangle locus changes as two lines are translated in the configuration. At the end of the video the hyperbola flattens. This locus, when completely flattened, is the image of a hyperbola under an affine transformation.
